Raising the bar: Speaking of Raising the bar…

By Dan Helgerson, Fluid Power Journal Technical Editor

I have an opinion about using bar vs MPa.

I have had the privilege of working on the equations for the International Fluid Power Society certification study guides. I was directed to do so using ISO standards where they applied. As a result, I had to learn to ride both horses, imperial (U.S. customary) and metric. Many others of us in North America have not had that experience. We prefer to convert all that metric stuff into imperial so we can do our calculations. We reluctantly, and out of necessity, have become almost comfortable with the bar as a unit of pressure because it is in such common use. We were just getting to the point where we could almost do some of the conversions in our heads, when we find we are expected to raise the bar (pun intended) and use the MPa. The MPa is an outsider, imposed on us, and it complicates many of our favorite equations.

But the bar is a convention, not a standard. For those of us who may be unfamiliar with the metric pressure units, they are the Pascal (Pa), equivalent to 0.000145 psi, the kilopascal (kPa), equivalent to 0.145 psi, and the Megapascal (MPa), equaling 145 psi. Somewhere between the kPa and the MPa is the bar, which equals 100,000 Pa or 14.5 psi.

So why is it called bar? The bar derives its name from the barometer. In 1665, Robert Boyle wanted to give a name to an instrument that had been invented years earlier by Evangelista Toricelli. The instrument was used for measuring the weight of air. Boyle joined together two Greek words to coin the term barometer, which means “weight measuring.” It was not until around 1900 that Vilhelm Bjerknes, the founder of the modern practice of weather forecasting, used the term bar as a unit of pressure, indicating the pressure exerted by air at a height of 111 meters (364 feet). This was the elevation where he did his research. However, atmospheric pressure is defined as the force per unit exerted by air at sea level, 111 meters lower than Bjerknes’ bar. So the bar is close to, but not equal to, one atmosphere.

Raise your hands. Given the equation F = pA and given the information that you must solve for F in Newtons with a 100 mm bore at 200 bar, how many of you will automatically convert the mm to inches and the bar to 14.5 psi, solve for pounds, and then convert the pounds to Newtons? Okay, I see those hands. Confession is good for the soul.

Even those of us who work with the bar must do a conversion to get the Newtons. The area of a 100 mm piston is 7,854 mm². Multiplying that by 200 bar, we get 1,570,800 units. But units of what? Mini-Newtons, macro-Newtons, fig Newtons? Hmmmm…

We can check our math by getting back into our comfort zone, solving for pounds, and then converting to Newtons. 100 mm / 25.4 = 3.937. Square this and multiply by 0.7854, and we find the area of the bore is 12.174 in². This times 2,900 psi (200 bar) = 35,303.8 pounds. To convert that to Newtons, we divide by about 0.225 and get about 156,905 Newtons. So with the rounding, we know our target answer is in the ballpark of 157,000 Newtons. When we compare the numbers, we see that our answer using mm² and bar is off by a factor of 10, so we must adjust our equation.

What if we change the mm to cm. That might help. 100 mm equals 10 cm, so my bore area will be 10 cm squared times 0.7854 or 78.54 cm². Multiplying 78.54 cm² x 200 bar gives us 15,708 units of something but still off by a factor of 10, just in the other direction.

It seems that, to get to where we want to be, we must divide something by 10 if we really want to keep the bar.

Dividing by 10 we find

or

Great! We now have the answer we were looking for and still used the bar. Success!

But wait a second. Isn’t

equal to 20 MPa? So

 

Am I saying that if we would just learn the equation F = pA where F is in Newtons, p is in MPa, and A is in mm², we could have solved the problem?

Yes!

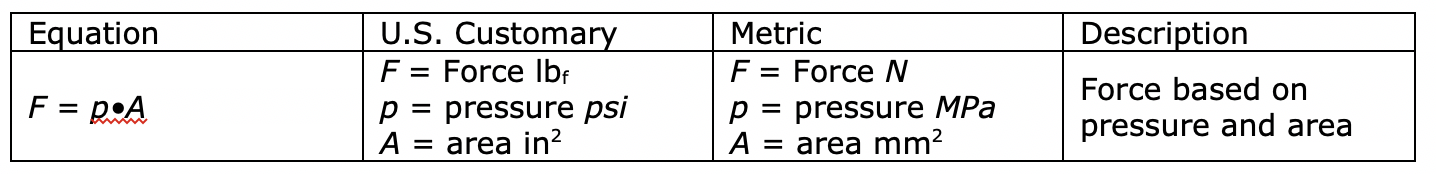
Or how about the equation for torque. We recognize it as

It works just fine in U.S. customary terms with T being torque in in.lb., p being psi, d being in³ displacement, and 2π being, well, 2π (6.2832). So, what if someone comes along and tells you that the metric equation has to be different? It must be

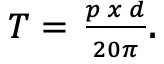
This is where T is torque in Nm, p is pressure in bar, and d is displacement in cm³. Using bar instead of MPa, the initial equation is off by a factor of 10. 2π has to be multiplied by 10 to accommodate the bad bar habit. Wouldn’t it be better to have one equation for torque that works with both metric and Imperial?

It is time to push away from the bar. After all, we may need to drive home. It is not time to reinforce old habits or stay trapped in the familiar. Sure, we old guys are most comfortable with the psi. We have come to tolerate the bar. We don’t like the MPa. But are we going to lead or are we going to follow?

It is time to raise the bar to the MPa.

---

Fluid Power Journal encourages conversation about issues addressed in “Raising the bar.” Please use the Comment function at the bottom of the page to take part in the discussion with author Dan Helgerson.