The diagram below represents a kid’s backhoe for a sand pile. I have converted it to work with pneumatics and placed the cylinders as shown. Calculate the lifting force at the tip of the bucket using the given information. You will need to use little trig on the last 5″ of the boom to get the horizontal distance needed for a moment equation.
There are multiple ways of solving this problem. I will show you a couple of them.
Metric
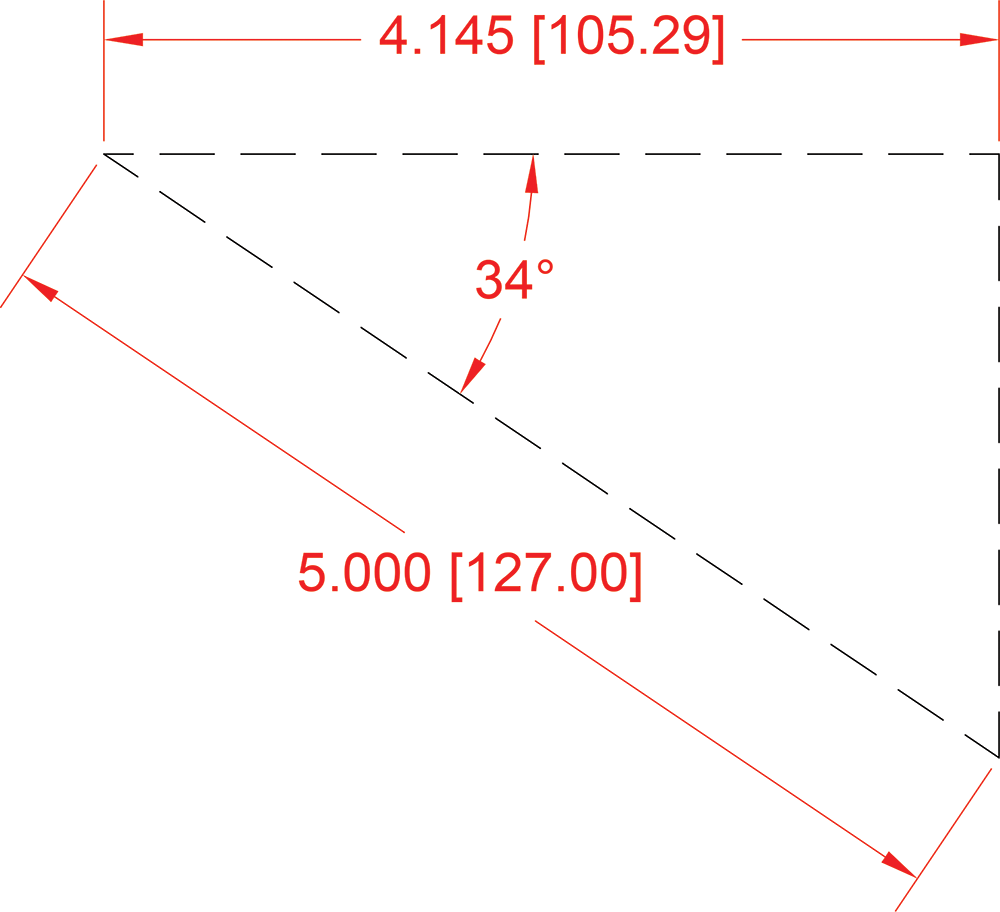
Step 1. Solve for the remaining horizonal distance from the end of the cylinder to the vertical arm on the boom. We can make a triangle using the 127 mm hypotonus and the 34°angle to get the rest of the horizonal distance. See diagram below. Cosine of the angle = the adjacent side divided by the hypotonus. Cosine of 34° = Y (adjacent side) / 127 mm. Cross multiplying = Cosine of 34° x 127 mm = 105.28 mm
Now add the 456.17 mm cylinder and subtract the 101.6 mm on the left side of the main beam and minus the 69.11 mm at the bottom of the bucket and you will get 392.3 mm (the horizonal distance).
Next, calculate the force on the cylinder. Diameter is 38.1 mm; therefore 38.1² x . 7854 = 1,140 mm² x .689 mPa = 785.46 N.
Let us write a moment equation since the both the load and effort are both perpendicular to the pivot:
177.8 mm x 785.96 N = 392.18 mm x N (Load)
N = 356.3 N x 4.448 = 80 pounds
Final Answer
A second way of solving the problem is with a mechanical advantage/disadvantage. Using the same number, the tip of the bucket has a horizontal distance of 392.3 mm and the cylinder has 177.8 mm vertical distance of leverage. Both the load and reaction are perpendicular to the pivot 392.3 / 177.8 = 2.206 mechanical disadvantage. The push on the cylinder is 785.96 N / 2.206 = 355.84 N.
Customary US
Step 1. Solve for the remaining horizonal distance from the end of the cylinder to the vertical arm on the boom. We can make a triangle using the 5” hypotonus and the 34°angle to get the rest of the horizonal distance. See diagram below. Cosine of the angle = the adjacent side divided by the hypotonus. Cosine of 34° = Y (adjacent side) / 5. Cross multiplying = Cosine of 34° x 5” = 4.145”.
Now add the 18” cylinder and subtract the 4” on the left side of the main beam and minus the 2.7 “ at the bottom of the bucket and you will get 15.445” (the horizonal distance).
Next, calculate the force on the cylinder. Diameter is 1.5”, therefore 1.5² x .7854 = 1.767 in² x 100 psi = 176.7 pounds of force.
Let us write a moment equation since the both the load and effort are both perpendicular to the pivot:
-7” x 176.7 pounds+ 15.445” x P (load) = 0
7 x 176.7 = 15.445P
1236.9 = 15.445P
P = 80 pounds / 4.448 = (355.84 N)

Final Answer
A second way of solving the problem is with a mechanical advantage/disadvantage. Using the same number, the tip of the bucket has a horizontal distance of 15.445” and the cylinder has 7” vertical distance of leverage. Both the load and reaction are perpendicular to the pivot. 15.445 / 7 = 2.206 mechanical disadvantage. The push on the cylinder is 176.7 lbs. / 2.206 = 80 lbs. (355.84 N).