Problem: Cylinder Retraction
Neglecting pilot line sizes, approximately how many seconds after pushing the start button will the cylinder start to retract?
See the Solution
We need to know a couple of basic things to solve this problem:
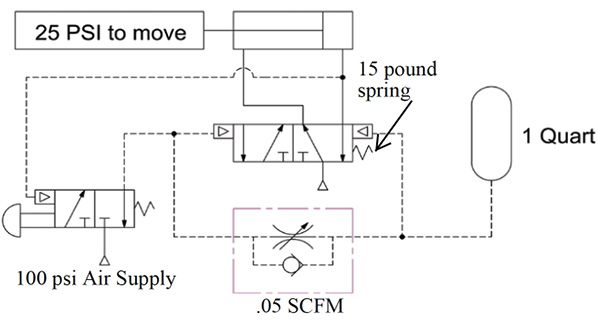
- How does the schematic work? The operator pushes the palm button that directs air to the pilot valve. This shifts the pilot valve to extend the cylinder. As the operator holds the button, the cylinder will extend, but also air is metered through the flow control to the one-quart air receiver and to the opposite end of the pilot valve. Note the 15-psi spring on that end. With an air supply of 100 psi, it will take a minimum of 85 psi (100 – 15) to start and shift the valve back to retract the cylinder if the push button remains held. This circuit is called a “pulse circuit” or a “one-shot circuit” where the cylinder will extend for a given period of time and then retract, even with the push button held down. Time is adjusted by changing the flow control or resizing the air receiver.
- Cubic inches in a quart: 4 Quarts = 1 Gallon; 231 / 4 = 57.75 cubic inches of compressed air.
- Next let’s find cubic inches of standard (free) air. One way of doing that is to find the compression ratio. This means how many cubic inches of non-compressed (SCIM) air it takes to get 57.75 cubic inches of compressed air to the pressure required to shift the valve back. One quick formula is (PSIG + 14.7) / 14.7. (85 + 14,7) / 14.7 = 6.78 : 1 compression ratio (CR). This means it takes 6.78 cubic feet of standard air to get 1 cubic foot of compressed air at 85 psig. Note: This is the same as a compression ratio on a car.
- Now convert 57.75 compressed cubic inches to standard cubic inches: 57.75 x 6.78 (CR) = 391.67 standard cubic inches.
- How many cubic inches per minute are filling the air receiver? Given .05 SCFM, therefore 1728 cubic inches in a cubic foot x .05 = 86.4 standard cubic inches per minute (SCIM).
- Let’s put this in a ratio: total air needed is to CIM as Time is to 60 seconds.
- 391.68 : Total Time 391.68 x 60 / 86.4 = 272 seconds to fill the receiver to 85 PSI
86.4 60 Sec.
Disclaimer: We are assuming no change in air temperature.
By Ernie Parker, AI, AJPP, AJPPCC, S, MT, MM, MIH, MIP, MMH, Fluid Power Instructor, Hennepin Technical College, EParker@Hennepintech.edu
This teaser is printed in the Fluid Power Journal. Those who submit the correct answer before the deadline will have their names printed in the Society Page newsletter and in Fluid Power Journal. The winners will also be entered into a drawing for a special gift.
5.2 seconds
The formula to use is: T = [V x( Pmax – Pmin) ] / 14.7 x Qscfm
Using the 231/1728 conversion formula, the quart has a capacity of .0334201 cubi feet.
T = [.0334201 (25 – 0)] / 14.7 (.05)
T = .8355025/ .735 =1.136738 minutes or 68 seconds required before the cylinder starts to retract.
T (Minutes) = [V acf x( Pmax – Pmin) ] / 14.7 x Qscfm
Using the (231 /1728)/4 formula, one quart has a capacity of .0334201 actual cubic ft
T = [.033 (86-0)] / 14.7 (.05)
T = 232 seconds before the cylinder starts to retract.
Cylinder starts retracted in this circuit. Pressing the start button extends the cylinder , 100 psi pilot holds the start button and starts a time delay to retract. The one quart bottle will need to reach 86 psi to shift the 5 way , exhausting the pressure from the start button pilot and 1 qt bottle. 86 psi + 15 psi spring = 101 psi . 5 way returns to its normal position with the cylinder retracted.
232 sectonds