What Blaise Pascal Never Told You

By Dan Helgerson.

Blaise Pascal, the French physicist, found that a confined fluid transmits externally applied pressure uniformly in all directions and that the resultant force is applied perpendicular to the walls of the container and is described as the pressure per unit area of the container walls.

It is from his research that we have what is probably the most important equation in all of fluid power; the simple formula of F = p • A where F = Force, p = pressure, and A = Area.

What Blaise never mentioned was that pressure times volume equals energy.

Energy is defined as the ability to do work. It could be kinetic energy that is doing work or potential energy that is waiting to do work. A confined fluid under pressure, whether flowing or static, has energy, which is the capacity to do work. E = p • V where E = Energy, p = pressure, and V = Volume.

Equation	Metric	US Customary
E = p • V	E = Energy Nm p = pressure MPa V = Volume cm³	E = Energy lbf.in. p = pressure psi V = Volume in³

This equation is changing the way we think about the transfer of energy through fluids.

Let me explain… and you might want to get out your calculator as we move through the explanation. 

In an electrical system there is generally a fixed voltage and the amount of work that can be done is determined by the available amperage. When you start up the grinding wheel on your workbench, a constant voltage is supplied to the motor and just the right amount of amperage passes through to maintain the rpm. When you begin to sharpen a tool, a new load is placed on the motor, but the voltage does not change. It is only the amperage that changes as the load varies.

In a fluid power system, the opposite happens. A fixed displacement fluid motor, hydraulic or pneumatic, having a constant rpm, must have a constant flow rate. As the load varies, it is the pressure that becomes the variable entity. 

Electrical System		Fluid System
Fixed Voltage		Fixed Volume
Kinetic Energy	Potential Energy	Kinetic Energy	Potential Energy
Variable Amperage	Stored Electrons	Fixed Flow	Fixed Volume

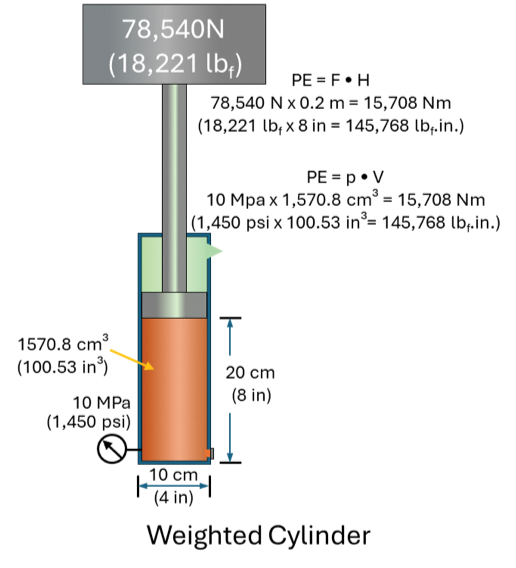
The graphic shows a weighted cylinder with both metric and US Customary dimensions (just so everybody can take part in the discussion). We know that the downward force (weight) times the height equals the potential energy (PE) in the load. A load of 78,540 N raised to a height of 0.2 meters will have a PE of 15,708 Nm. Doing the math with pounds and inches we find a PE of 145,768 lb_f.in. No surprise there.

Dividing the load by the piston area will provide the pressure (p = F / A). But this is what Blaise Pascal never told you: If you take the volume of fluid under the piston and multiply it by the pressure, you will find that the PE in the fluid is exactly the same as the PE in the load. A pressure of 10 MPa acting on 1,570.8 cm³ produces a PE of 15,708 Nm. 1,450 psi acting on 100.53 in³ produces a PE of 145,768 lb_f.in. Each cm³ is charged with 10 Nm of energy. Each in³ is charged with 1,450 lb_f.in. of energy. The pressurized volume is made up of energy units (U_E), MPa/cm³ or Nm, psi/in³ or lb_f.in.

Weighted Accumulator
	Bore cm/in	stroke cm/in	Load N/lbf	Pressure MPa/psi	Volume cm³/in³	PE (FxH) Nm/lbf.in.	PE (pxV) cm³/in³
Metric	10	20	78,540	10	1570.8	15,708	15,708
US	4	8	18,221	1,450	101	145,768	145,768

Now this should come as no surprise. It makes perfect sense that the energy in the fluid must equal the energy in the load, but this is something that most of us have not been asked to consider. We will see how our lack of attention to these energy units (U_E) has caused much of the waste in our fluid power systems.

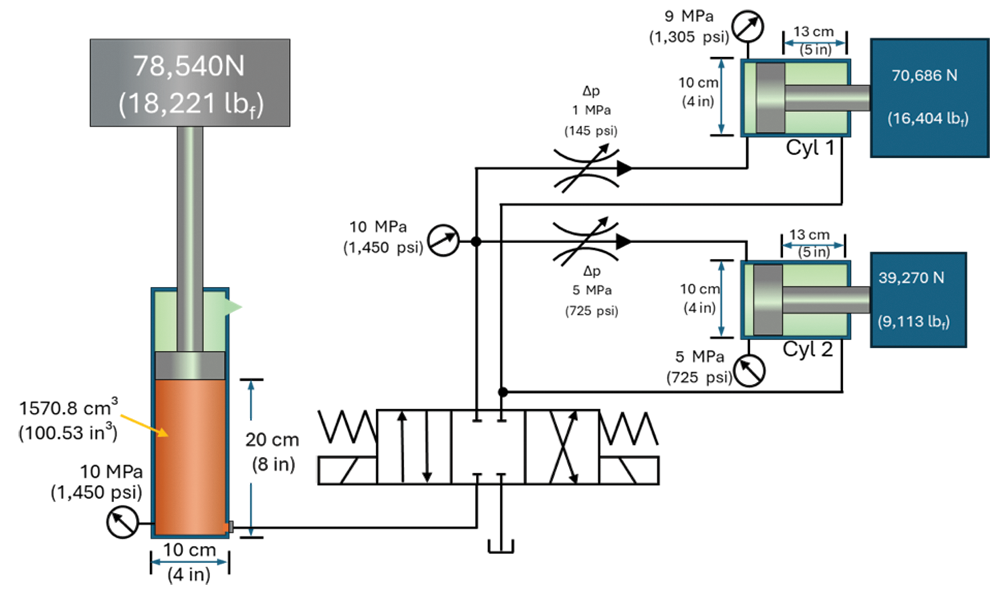
In the example, we are going to use the stored UE in the weighted cylinder to synchronize and control the extension speed of two cylinders, each with a different load.

Cylinder 1
	Bore cm/in	stroke cm/in	Load N/lbf	Pressure MPa/psi	Volume cm³/in³	Energy Needed	Energy Used
Metric	10	13	70,686	9	1,021.0	9,189	10,210
US	4	5	16,404	1,305	63	82,020	91,105
Cylinder 2
	Bore cm/in	stroke cm/in	Load N/lbf	Pressure MPa/psi	Volume cm³/in³	Energy Needed	Energy Used
Metric	10	13	39,270	5	1,021.0	5,105	10,210
US	4	5	9,113	725	63	45,565	91,105

	Required Volume cm³/in³	Available Volume cm³/in³	Difference
Metric	2,042	1,570.8	-471
US	126	101	-25

To extend these cylinders, we are conditioned to think only of the volume, separate from the pressure, and so we conclude that we do not have enough fluid. According to the chart, we have an available volume of 1,570.8 cm³ (101 in³) with a required volume of 2,042 cm³ (126 in³). We come up short by 471 cm³ (25 in³). We will have to extend the weighted accumulator an additional 6 cm (2.4 in).

But now we have learned to ask the question, “Is there enough energy to extend the cylinders?” When we combine pressure and volume to determine energy, we find that we have 15,708 Nm (145,768 lb_f.in) U_E available. Only 14,294 Nm (127,585 lb_f.in.) U_E are needed. We have an excess of 1,414 Nm (18,183 lb_f.in.) U_E.

	(UE) Needed Nm/lbf.in.	Available UE Nm/lbf.in.	Difference
Metric	14,294	15,708	1,414
US	127,585	145,768	18,183

We clearly see that we have plenty of energy, but how do we access it? Blaise Pascal never told us to think about energy units and so we have not developed a mechanism for extracting the extra energy in the system, until now. On the horizon is the new Variable Displacement Power Controller (VDPC) that will enable us to produce energy at one power density (pressure times volume) and then reconfigure the energy to the power density needed for the work. 

For Cylinder 1, the VDPC would take 918.9 cm³ @ 10 MPa (57 in³ @1450 psi) from the weighted accumulator and reconfigure it to 1,021 cm³ @ 9 MPa (63 in³ @ 1305 psi).

For Cylinder 2, the VDPC would take 510.5 @ 10 MPa (31 in³ @ 1450 psi) from the weighted accumulator and reconfigure it to 1,021 cm³ @ 5 MPa (63 in³ @ 725 psi).

The total volume taken from the Weighted accumulator would be 918.9 cm³ + 510.5 cm³ = 1,429 cm³ (57 in³ + 31 in³ = 88 in³). The accumulator held 1,570.8 cm³ (101 in³). 1,570.8 cm³ – 1,429.4 cm³ = 141.4 cm³ (101 in³ – 88 in³ = 13 in³).

By using pressure and volume instead of just volume, and having the right tool, we can more efficiently use the available energy and maintain a smaller stored volume.

In addition, the VDPC replaces the pressure compensated flow controls by reconfiguring the power leaving the accumulator to the power required by the cylinder.

Some terms and concepts that may be unfamiliar but that must become part of our fluid power vocabulary:

U_E = Unit of energy; the pressure times the unit volumes as measurements of the ability to do work. In the metric system it is the MPa × cm³ or Nm. In US Customary it is the psi × in³ or lb_f.in.

U_P = Unit of power; the pressure times the flow rate. In the metric system, MPa × lpm, which can be translated to kW by dividing by 60. In US Customary, psi × gpm, which can be translated to hp by dividing by 1714.

Power density; the relative amount of pressure in the flowing fluid. Higher pressure means higher power density.

Energy density; the relative amount of pressure in the fluid whether flowing or static. Higher pressure means higher energy density.

Flow control is power control. To produce flow there must be a pressure differential (Δp). Pressure × flow requires power. Therefore, flow control is power control. A flow control valve limits the power going to an actuator.

If you are interested in more information about this article or about the VDPC, please contact me at Dan@Perisseuma.com.