What in the World Do Those Numbers in the ISO Cleanliness Code Mean?

We have been talking a lot about filtration here at the steel mill. My predecessor, Scott McLoughlin, had done a remarkable job in educating by example, demonstrating the need for good control of the fluids in our hydraulic and lubrication systems. He had helped stop the leaks and had added well thought-out filtration systems that have resulted in substantial savings and increased productivity. There is still a lot of work to be done, and in pursuing that, we have invited a number of vendors in, each offering an approach to getting and maintaining an acceptable fluid cleanliness level. The one thing they all have brought to the table is a discussion of the ISO cleanliness code. I was in a meeting with a group of managers when one vendor began to talk about the code. Being a Certified Fluid Power Accredited Instructor (AI), I immediately saw this as an obvious teaching moment, so I asked, “Does anyone here want to know what those numbers mean?” The answer was a quick and resounding, “No!”

Now, if you are a fluid power professional or aspire to be one, you do not have the luxury of willful ignorance. The ISO cleanliness code is the industry standard, and we ought to know what it means. This article becomes my replacement teaching moment.

The industry has known for a long time that contamination is the major cause of failure in fluid power systems. The challenge has been to come up with a standardized method of measuring and describing the cleanliness of the fluid and then to establish guidelines for determining just how clean the fluid ought to be for a given system. 

Having a filter, even the best filter, does not ensure clean fluid. If the filter is bypassing or in the wrong location, it will not protect the components. The only way to be sure of the contamination level of the fluid is to take a sampling of the fluid as it moves through the system. It is important to get the sample out of the working fluid because fluid that is at rest, like in the reservoir or during a shut down, will not give an accurate picture of what is happening dynamically.

We also need to understand something about contamination. It is not like there are a bunch of little tiny ball bearings of uniform shape and size in the fluid. Contamination is the debris resulting from wear, assembly, dust in the air, and/or anything else that can break loose and be caught up in the fluid stream.  The particle sizes range from itty-bitty to big chunks, and the shapes are irregular. 

It was found that, by looking at particles in three different size groups and then seeing how many of those particles were in a specific volume of fluid, we could make an evaluation of the overall condition of the fluid. The sizes chosen are 4, 6, and 14 micrometers. Micrometers are also referred to in terms of microns and use the symbol µm. The volume of fluid to be sampled is 100 ml (a little less than ½ cup). 

It is important to note that these are very small particles, all of which are smaller than can be seen by the unaided human eye. We can see particles that are as small as 40 µm. The stuff we are talking about is 3 to 10 times smaller than anything we can see. A red blood cell is about 8 µm in size, and when was the last time you could pick one of those out in a crowd?

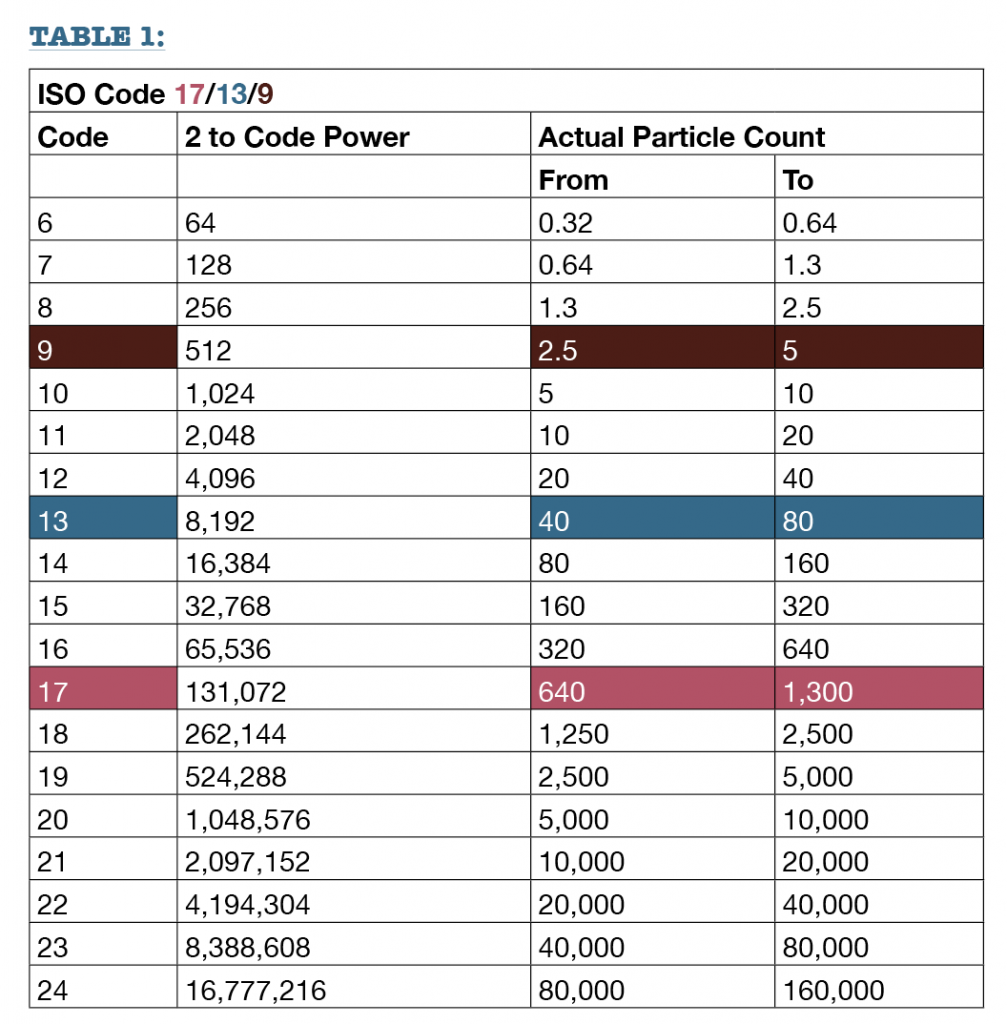
A fancy machine looks at the sample and counts the particles it sees. This is where it starts to get fuzzy, so hang on. We are not given the actual particle count. Instead, the count is described in terms of how it relates to the factor of 2. For example, if there were 512 counted particles in a 100-ml sample of fluid, there would be 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 (or 2⁹) number of particles and we are given the number 9 as the count. 

I see some of you just dropped out. It’s really not that bad. Take a moment and read the last paragraph again, slowly…ok, now, do you understand what the number 9 represents here? That’s right! It is the number of times 2 would be multiplied by itself to equal the particle count. Now, I don’t pretend to know why this approach was chosen, but it is what we have to live with.

But wait! There’s more. The number 9 does not mean that there are 512 particles that were counted. It means that there were between 2⁸ and 2⁹ particles counted or somewhere between 256 and 512 particles. Adding another layer of complexity, what is published is the maximum contamination level expected to be found in only 1 ml (1/100^th) of the sampling. So, when we look at the data, we are to understand that the 9 means that we can expect to find between 2.5 and 5 counted particles in every 1 ml of fluid. Huh??? 

I can repeat that but instead, let me give you an example. Let’s say we have a test result that shows a cleanliness level of 17/13/9. What does that tell us, exactly?

Well, it doesn’t “exactly” tell us anything. What it gives us are two categories for describing the cleanliness of the fluid. It provides information on the size and quantity of particles in the system. The first number represents the range of particles that are 4 µm (micrometers) or larger in 1 cc (1 ml) of a sample fluid but not a precise number of those particles. The first number will never be smaller than the second number, and the second number will never be smaller than the third number because each number includes the particles in the next group.

The second number represents the range of particles that are 6 µm and larger.

The third number represents the range of particles that are 14 µm and larger.

Remember, the number is the power to which 2 is multiplied. That result is then divided by 100 and rounded a little bit to give the maximum number of particles of a certain size and larger that you would expect to find in 1 cc (1 ml) of fluid. The actual particle count would be somewhere between ½ of that number and that number. 

In a 17/13/9 result, we have a particle count, including all sizes 4 µm and larger represented by 17. That means we have a maximum number of particles 4 µm and larger of 2¹⁷/100. 2¹⁷ = 131,072. If we divide that by 100, we get 1,312. So the maximum number of particles 4 µm and larger in the 1 cc sample would be 1,300. (Remember the rounding?) The minimum number of particles 4 µm and larger would be 2¹⁶/100 or 655 (but because of the rounding, the number used is 640). The bottom line is that the 17 tells us that we have somewhere between 640 and 1300 particles 4 µm and larger in a 1 ml sample.

Continuing, the 6 µm and larger particle count is represented by 13 so the number of particles 6 µm and larger is somewhere between 2¹²/100 and 2¹³/100. 2¹² = 4,096. If we divide that by 100, we get 41ish. 2¹³ = 8,192. When we divide that by 100, we get 82ish. So the total number of particles in the 1 cc sample 6 µm and larger would be anywhere between 40 (Remember the rounding?) and 80.

The 14 µm and larger particle count is represented by 9, so the number of particles 14 µm and larger is somewhere between 2⁸/100 and 2⁹/100. 2⁸ = 256. If we divide that by 100, we get 2.5ish. 2⁹ = 512. When we divide that by 100, we get 5ish. So the total number of particles in the 1 cc sample 14 µm and larger would be anywhere between 2.5 and 5.

This is where we need to be careful. The difference between 17/13/9 and 18/13/9 could mean as many as 1,200 more particles or it could mean just 1 more particle. That is why it is important to get sampling over time.

Table 1 shows the code numbers and what they mean. The number color matches the highlighted row on the table.

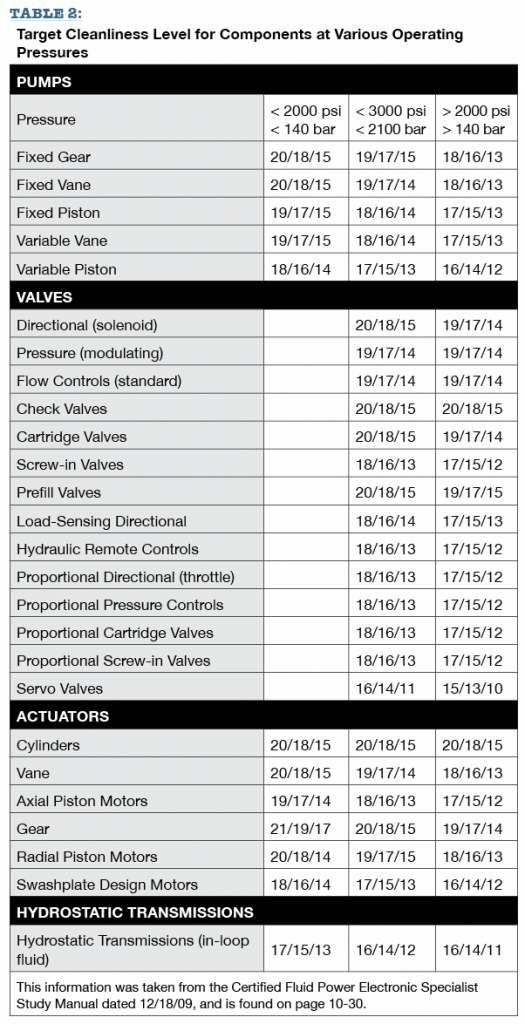
Now that we have a way of describing the contamination level, how do we determine what the level ought to be? Different components have a different tolerance for contamination. A system with a gear pump, poppet valves, and cylinders will not require the same cleanliness as a system using piston pumps, servo valves, and piston motors. Studies were done to determine the cleanliness level required for various fluid power components. This resulted in Table 2, which helps us know how clean a particular system needs to be. We can now set a target cleanliness level based on the contamination tolerance level of the most sensitive component in the filtered fluid stream. We can also isolate and target super sensitive components and provide them with their own dedicated filtration systems.

• career
• cleanliness code
• contamination
• dan helgerson
• education
• fundamental
• iso
• professional
• safety