Transforming Applications

Fluid power has become a vital component in our ability to perform work: it harvests our crops, takes our waste to the landfill, moves the landing gear, entertains and protects us, and all with a power density and flexibility that is unmatched in any other power transfer system. However, when it comes to efficiency, fluid power systems are not very high on the list. This article series will ask us to think differently about our fluid power systems. We will look at energy in a different way and discover ways to transform fluid power energy to make our systems more efficient, and then be able to make better use of the new and improved components available to us.

For many of us, the concept of using a Variable Displacement Transformer (VDT) is new and a little unsettling. In this article, we will set up a VDT circuit using a step-by-step process based on what we have already learned.

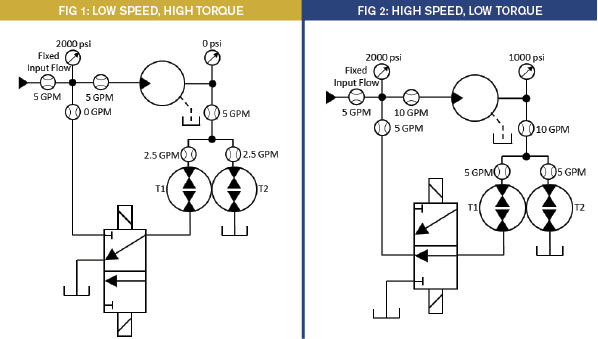
In the article “Divide and Conquer (January/February 2017 issue),” we discussed a system using a 50/50 transformer to provide a two-speed, two-pressure system for a hydraulic motor (application 8). The system had a constant flow source, and the transformer was placed at the outlet of the motor. During the low-speed, high-torque portion of the cycle, all the exhaust flow was directed through the transformer with one section (T2) open directly to the reservoir and the other (T1) open to the reservoir by way of the directional control valve. For this discussion, we will assign an inlet pressure of 2000 psi and an inlet flow of 5 gpm. The pressure at the inlet is what is needed to provide the torque. The pressure at the outlet is near zero, and so there is little resistive load from the fluid on the motor. It is almost like the transformer is not even there.

During the high-speed, low-torque portion of the cycle, the outlet flow from T1 is directed through the directional valve to join the flow from the source, and the inlet pressure to the transformer became 0.5 x the inlet pressure to the motor… Ok, Ok, I know, I am going too fast. Let me explain. The transformer acts as a pressure intensifier. We know the outlet of T1 is now connected to the inlet of the motor, which has a pressure of 2000 psi. Being a 50/50 transformer, its inlet will have to be one-half the pressure of the outlet at T1 as long as T2 is directed to the reservoir. Energy in has to equal energy out. This causes a back pressure on the motor of 1000 psi, reducing the available torque. The combination of regenerated flow from T1 and consequent back pressure produces the high-speed, low-torque portion of the cycle.

In Figures 1 and 2, we are using a 50/50 transformer, but an application is not limited to this ratio. What would be the result if we were to use a 60/40 transformer where 60% of the input flow passed through T1? We call the flow from the source Qs and flow to the motor inlet Qi. The percentage of flow going to the reservoir will be referred to as T2. The equation for the input flow will be

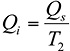
Before the directional valve is shifted to send fluid to the pressure line, the 60/40 is just like the 50/50—it has no effect. But when the valve is shifted, the input flow using a 60/40 transformer with a source flow of 5 gpm would be Qi = 5 gpm ÷ 0.4 = 12.5 gpm. The effective pressure times the displacement determines the available torque, and the effective pressure will be the inlet pressure minus the opposing outlet pressure. If we call the inlet pressure pi and the effective pressure pE, we can determine the effective pressure by using the equation pE = pi T2 . PE = 2000 psi x 0.40 = 800 psi. So, the input flow would increase by 250%, and the available torque would be reduced to 40%.

Now we will change the application to one where we have two discrete torque requirements but also need to maintain a constant 1000 rpm. (See Figures 3 and 4.) The fixed flow source will be replaced with a variable-displacement, pressure-compensated pump. Half of the time the system will operate at high torque, and half of the time it will operate at low torque. We will assign a displacement value of 10 cc to the motor and a maximum pressure requirement of 21 MPa and a minimum requirement of 10.5 MPa. The pressure compensator will have to be set for the highest torque requirement plus 1.5 MPa so that the pump does not begin to compensate too soon. A pressure-compensated flow control (power control) will have to be installed to maintain the constant RPM.

When we think in terms of Units of Power, in this case kW, we see that the motor will require a power rate of 21 MPa x 10 lpm ÷ 60 or 3.5 kW at high torque. It will require 10.5 MPa x 10 lpm ÷ 60 or 1.75 kW at low torque (see discussion on energy units in the “Flow Means Go… Well Not Exactly” article in the September/October 2016 issue). The pressure-compensated pump with the pressure-compensated power control supplies a constant 3.75 kW (22.5 MPa x 10 ÷ 60). There is a loss of 0.25 kW during the high-torque cycle and a loss of 3.4 kW during the low-torque cycle. The average energy requirement is 1.92 kW. There is an average waste of 1.82 kW. In addition, there is a constant energy loss through the case drain of the pump, amounting to about 5% of the full load capacity.

When we divide the average energy requirement by the energy input, 2.62 kW ÷ 3.75 kW, we have an efficiency of 70%. When we take away the 5% case drain flow, we have an overall hydraulic efficiency of 65%. By current standards, this is pretty good. But we should not be satisfied. We can do better.

We will introduce the 50/50 transformer into the system.

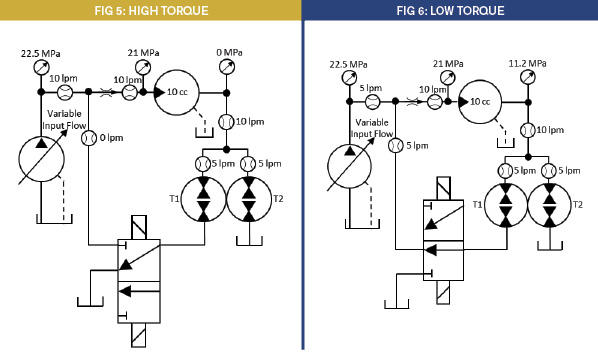
As you can see in Figures 5 and 6, during the high-torque cycle, the energy usage is the same as it is without the transformer. But during the low-torque cycle, the transformer regenerates half the flow back into the supply. This produces the necessary back pressure to reduce the torque, but notice what happens to the flow from the pump. The pump flow is reduced by the amount of flow from the transformer. The source flow is now only 5 lpm at 22.5 MPa. This is because the pressure-compensated flow control will only allow 10 lpm to pass through it. By regenerating 5 lpm to the inlet, the pump has to de-stroke and supply only the make-up fluid to satisfy the power control.

The power requirement is cut in half, and the power from the source is also cut in half. The resistive pressure that reduced the available torque is regenerated to feed the supply. The result is an energy loss during the high torque of 0.25 kW and an energy loss of only 0.125 kW during the low-torque cycle. The average energy loss is only 0.188 kW, as opposed to 1.82 kW without the transformer. Very few systems operate at discrete power levels. Using the multi-section transformer is useful in some applications, but what about loads that constantly vary from one extreme to another? We have seen the characteristic of the fixed-displacement transformer that causes the variable source to only supply the energy units needed to do the work, but it is limited to discrete ratios based on the displacements and number of sections. 

This is where we can introduce the Variable Displacement Transformer (VDT) where the ratios can be infinitely varied to match the energy requirements at each moment of operation. The following illustrations show the same application at maximum and minimum torque with the VDT only requiring the units of power needed for the work. The pressure-compensated power control has been replaced. Instead, we are allowing the output flow from the fixed-displacement motor, corresponding to the RPM, to determine the ratios of the transformer.

In the circuit in Fig. 7, we show the same pump and motor combination as before, but we have introduced the VDT system at the outlet of the motor. The motor exhaust passes through an adjustable orifice. The pressure differential across the orifice responds to the outlet flow of the motor. The motor is of fixed displacement, and so the outlet flow is proportional to the RPM of the motor. The compensator of the transducer is set at 5 bar, and so the adjustable orifice is set so that a flow of 10 lpm produces a Δp of 5 bar. The default status of the transformer is for T2 to be at 100% and T1 is at 0%; in other words, at the high-torque position. As the load decreases on the motor, it will try to increase its speed because of the constant input power from the pump. But the increase in speed produces an increase in the Δp, causing the transformer to begin regenerating flow to the inlet of the motor. The transformer will continue to shift until the flow through the motor is reduced back to 10 lpm. Notice in the circuit that the regenerated flow is 0 and the pump flow is 10 lpm at 21 MPa. We have maximum power producing maximum torque. As the load continues to decrease, the regenerated flow approaches 9 lpm and the flow from the pump approaches 1 lpm, all the while maintaining the constant RPM of the motor.

Hold on there! Are you telling me that 1 lpm from the pump is going to produce 10 lpm to the motor? That’s crazy!

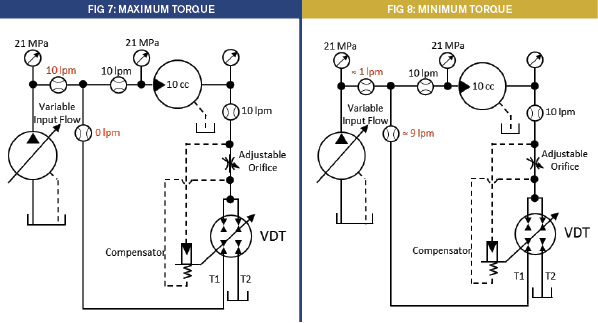
It sounds crazy as long as we still think of flow and pressure separately. We need to combine them as units of power. The VDT has now modulated to a ratio of 90/10. That means the effective pressure is going to be pE = pi T2 = 21 MPa x .1 = 2.1 MPa. (See Fig. 8.)

The VDT transitions the circuit from being fully open, where all flow from the motor is directed to the reservoir, to being fully closed where all flow from the motor is returned to the motor. This has the effect of varying the available torque from maximum to zero. The units of power required from the source are only those needed to make up the power to drive the load.

The power needed to rotate the motor with this low torque is 2.1 MPa x 10 lpm ÷ 60 = 0.35 kW. The pump is supplying 21 MPa x 1 lpm ÷ 60 = 0.35 kW. The source power is exactly what is needed. It has just been transformed.

• dan helgerson
• transforming applications
• transforming fluid power
• watts it all about