All About Vacuum: Basics a Mystery for Many Pros
By Daniel Pascoe, President, Davasol Inc.
As a technology, vacuum is bundled into fluid power with pneumatics and hydraulics. That’s why you’re reading this article in Fluid Power Journal. But if vacuum is thrown in with fluid power, how come so few professionals understand it? Most know that many applications work alongside vacuum products. But vacuum is often misunderstood or ignored completely because “it works.”
This article reviews some basics, looking at what vacuum is and how it works in fluid power applications.
Vacuum can be defined as “a space entirely devoid of matter.” But a better explanation might say that vacuum is a known volume that has a lower pressure than that which immediately surrounds it. An example is the inside of a suction cup when it is sealed against a surface.
But how exactly does vacuum work, and how is it used in industrial applications?

Figure 1

Figure 2
How vacuum works
To help visualize my definition of a vacuum, figure 1 shows a tank that’s been filled with air molecules at atmospheric pressure and then sealed. A vacuum pumping device (like the venturi shown in figure 1) removes some of the gas molecules. This creates the vacuum (lower pressure) in the tank. The vacuum gauge shows the level of vacuum as it increases from zero and is now at 27 inches of mercury. If using a pressure gauge, the pressure would begin at atmosphere and decrease toward zero.
Units of measure
Figure 3 is a linear table of vacuum measurement units. Remember that, in an absolute pressure scale, indicated in the figure by (a), zero is absolute, a complete vacuum, “a space entirely devoid of matter.”

Figure 3
Inches of mercury, the most common unit of vacuum measurement in North America, could also be called pressure differential. When there is no vacuum, i.e., no change from atmospheric pressure, the reading on a vacuum gauge is zero, as shown in figure 1. As the pressure in the tank reduces, the vacuum level increases.
Torr is pressure measurement that uses the height of a column of mercury in millimeters, with 760 Torr being 1 atmosphere. As the pressure in the tank reduces, the Torr value decreases, with zero indicating a complete vacuum. 27” Hg equals 76 Torr. Another pressure measurement is the millibar (mbr), where 1013 mbr is 1 atmosphere. 27” Hg is 100 mbar. Both Torr and mbar measure gas pressure, whereas inches of mercury (“Hg) and minus kilopascals (-kPa) measure vacuum from a differential pressure reference, i.e., the difference from atmospheric pressure.
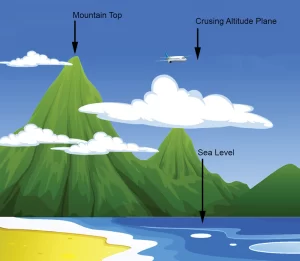
Figure 4
But what creates the vacuum force? Air around us has pressure that applies a force on the surface of an object. The taller the column of air, the greater the pressure. Imagine a column of air at sea level. The pressure at sea level is 14.7 psi (or 1 atmosphere), but as the column’s height decreases, the pressure also decreases. This is illustrated in figure 4, where at the summit of Mount Everest – 29,000 feet – the atmospheric pressure is only 4.5 psi. A plane with a cruising altitude of 37,000 feet has an atmospheric pressure of only 3.1 psi. Mexico City has an average atmospheric pressure of 11.1psi.
Why is that even relevant? Vacuum pick and place machines are less effective in Mexico City than in New York City. Here’s why.
A vacuum cup does not suck itself against the product it is picking up; it is pushed against the product by atmospheric pressure. The lower the atmospheric pressure, the lower the potential clamping force of the vacuum cup. As shown in figure 5, on the cup sealed against a surface, the vacuum is off. Turning on the vacuum reduces the pressure inside the cup. The higher atmospheric pressure pushes the box up against the cup and pushes the cup down onto the box. The cup is clamped by the higher atmospheric pressure on the outside pushing up and down. That is why the cup collapses. It is not being sucked down; it’s being pushed on.

Do the math
How much weight can a suction cup lift or grip? Manufacturers use a simple calculation. Assume the cup is 2 inches in diameter. Find the area of the cup face on the product with the equation A = πr² where A is the area, π is 3.142, and r is the radius, which is ½ the diameter.
A = 3.142 x (0.5 x 2 in)2 = 3.142 square inches
According to the chart, the differential pressure between atmospheric and the pressure under the cup is about 13 psi. Reduced from 14.7 to 1.7 psi inside the cup, the differential pressure is 13 psi. A 3.142 square inch cup is:
3.142 (area) x 13 (differential pressure) = 40.85 pounds
That’s how a suction cups works in a theoretical lifting application. If you have an eight-pound box, use four cups that can lift at least 10 pounds each, one in each corner. A safety factor is your choice. Personally, I use as much as the customer can afford, but a factor of at least 6:1.
We’ve discussed some basics about vacuum versus atmospheric pressure. The type of pump, cup, and vacuum control also affect efficient vacuum pick and place systems.
This article is the opinion of the author, Daniel Pascoe, president of Davasol Inc., an industrial brand management firm. One of Davasol’s clients, Vacuforce LLC, based in Indianapolis, partnered with the author on this article. Contact Daniel Pascoe at dpascoe@davasol.com.