The Science of Vacuum-Cup Forces

By Dane Spivak, Engineering Manager, Davasol Inc.

Force generated by vacuum is not an alien concept. It is something we experience throughout our lives, whether it is putting a hand over a vacuum cleaner nozzle or drinking from a straw. We observe it regularly. But how can we break it down to understand, measure, and predict its affects? This article dives into exactly what vacuum is and how it generates force for vacuum cups to grip a surface.

Vacuum can be defined on earth as a pressure lower than atmospheric pressure in a known volume, atmospheric pressure being the datum point of measurement. The most common vacuum unit of measure used in North America is inches of mercury (inHg), but for the sake of this exercise we’ll use psi because it is more familiar in fluid power. Standard atmospheric pressure at sea level is 14.7 psi. This pressure is created by the weight of the air around us, which can change depending on the altitude and weather. To create a vacuum, a pressure lower than the atmospheric must be generated to establish a differential.

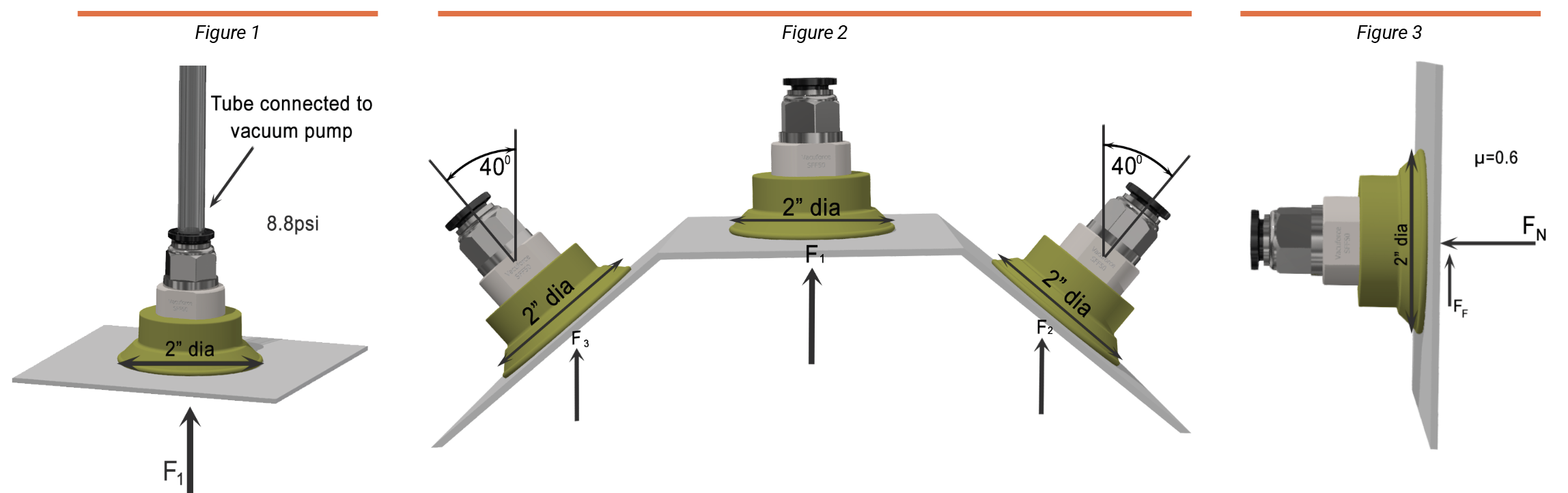
Figure 1 shows a 2-inch diameter, or 1-inch radius, vacuum cup connected to a tube placed on a glass surface. This is our known volume. If you attach a vacuum pump to the tube that generates a 60% vacuum, reducing the pressure inside the cup, the pressure inside the cup decreases to 5.9 psi, and therefore the differential from atmospheric pressure results in 8.8 psi. This 8.8 psi differential pressure – the difference between the pressure inside the cup and the atmospheric pressure outside the cup – is what we use to calculate the holding/gripping force of the vacuum cup. Force is the result of pressure multiplied by area. In the following example, the area is the circular 2-inch diameter vacuum cup, and the vacuum pressure is the differential pressure. The calculations show the holding force in pounds that the vacuum cup exerts coupled to the vacuum source.

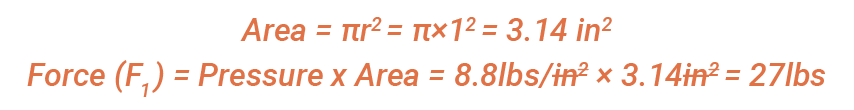
From a physical perspective, the atmospheric air pressure under the glass is pushing the glass up against the cup because there is a lower pressure inside. Therefore, vacuum force is limited by the available atmospheric pressure. If the atmospheric pressure is less, such as an area at altitude, then the applied force to the glass would be lower if the pressure inside the cup remained the same. The take away is that vacuum force from a suction cup is dependant on atmospheric pressure, vacuum-generated pressure inside the cup (vacuum level), and the area of the cup where vacuum is applied to the surface.

Figure 2 shows three 2-inch cups gripping a part, with two of them at a 40° angle. In this example, the cups intend to move directly upward when gripping the part. As we learned from figure 1, we can calculate the lifting force of the middle cup. However, the two outer cups are angled, which affects the amount of vacuum force being applied vertically. Sticking to our differential vacuum pressure of 8.8 psi, we know that the full area of a 2-inch cup applies a force of 27 lbs. But the angled cups apply less vertical lifting force as indicated by the vector arrows in figure 2. The calculations show the affects:

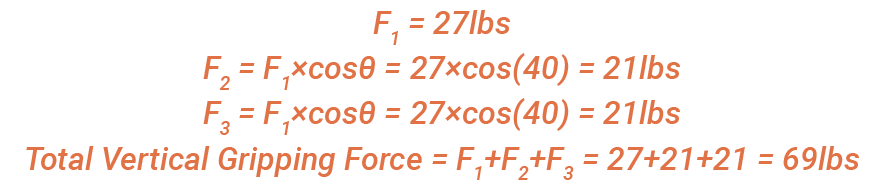
Now consider a full-shear application in which a cup is gripping a part at a 90° angle. From the calculations of figure 2, the angle would go to 90° and therefore zero the force from those cups. But intuition tells us that in a real-life situation, the part could still provide a vertical lifting force because figure 2 ignores the frictional force between the cups and the surface.

In figure 3, the same 8.8 psi and 2-inch cup generates a vacuum gripping force of 27 lbs. The amount of friction force is based on two factors. One is the vacuum gripping force, which applies a force that is 90° to the friction surface. This is typically referred to as the “normal force” when describing friction. Secondly, the coefficient of friction, known as Mu (µ), defines the percentage of the normal force exerted as friction. Coefficients of friction depend on the interaction of the cup with the product surface and how well or poorly they create friction. For example, a rubber cup on a smooth glass surface has a high coefficient of friction, whereas an oily metal sheet has a lower value as it is more likely to slip. The µ value can be found experimentally, though typical shear-gripping applications implement additional safety factors instead of calculating this value. The calculations based on figure 3 demonstrate the frictional force. In this example, we chose the µ value arbitrarily and ignored weight and other external forces.

As we see in the calculation from figure 3, the friction force delivers a significant impact to the applied forces of a vacuum cup. So the force created by the vacuum-level pressure and friction each contribute to the output.

Figure 4 uses the same criteria as figure 3 but at an angle of 40°. This allows us to calculate the impact of both forces. Again, we’ve ignored weight and other external forces.

Vacuum-cup forces are generated by vacuum pressure and friction, which can be calculated for theoretical numbers. However, based on the application and product being gripped, there are other underlying factors to consider, and the appropriate safety factors and designs should be implemented. This article showcases concepts only. Reach out to a professional for your application needs.

This article is the opinion of the author, Dane Spivak of Davasol Inc., an industrial brand management firm with many clients. One of Davasol’s clients, Vacuforce LLC, based in Indianapolis, partners with the author on this article. Contact Dane Spivak at dspivak@davasol.com.