IFPS Upgrades Hydraulic Specialist Certification
The Upgraded Hydraulic Specialist (HS) Certification Study Manual has been released and is available by visiting www.ifps.org. The IFPS HS certification is for those designing hydraulic systems and writing specifications, sizing, and selecting components for mobile and industrial industries.
Candidates may register now for the HS certification test by visiting www.ifps.org; testing for the HS certification begins April 1, 2017. The three (3)-hour written HS test contains 50 multiple choice questions.
“To keep pace with changing fluid power and motion control technologies, IFPS is committed to reviewing our certification study manuals and tests every five years by a panel of subject matter experts. All material is reviewed for relevance and current technical best practices and standards,” said Donna Pollander, ACA, IFPS executive director. “What the IFPS provides in our newly updated HS study manual and certification test is a highly developed, vendor-neutral, benchmarking tool to evaluate an individual’s fluid power competence, knowledge, and skill set.”
The upgraded HS study manual contains five sections of tasks with outcomes, as well as review questions and pre-test practice questions for the following domains:
- Understanding the Function Of Hydraulic Components In Circuits
- Analyzing Loads and Motion
- Selecting Components for Hydraulic Systems
- Analyzing and Troubleshooting Hydraulic Systems
- Electrohydraulic Control Systems
Special Thanks
Thank you to the following volunteer subject matter experts and consultants who helped refine the upgraded HS certification:
Thomas Blansett, CFPAI, Consultant
Dan Helgerson, CFPAI, Consultant
Rance Herren, CFPSD, National Oilwell Varco
John Juhasz, CFPS, Kraft Fluid Systems
Sam Kaye, CFPS, Ensign Energy Services
Thelma Marougy, Thema Consulting LLC
Ernie Parker, CFPAI, Hydra Tech, Inc.
Mark Perry, CFPHS, Fitzsimmons Hydraulics Inc.
Denis Poirier, Jr., CFPAI, Eaton Corporation
Elizabeth Rehfus, CFPE
Bob Sheaf, CFPAI, CFC Industrial Training
Neil Skoog, CFPAI, ERHCO
Timothy White, CFPAI, The Boeing Company
Test Your Skills
a. 7.2 cc, 11 lpm
b. 12.4 cc, 19 lpm
c. 38.0 cc, 59 lpm
d. 69.1 cc, 107 lpm
e. 456.2 cc, 707 lpm
a. 0.0014 MPa.
b. 0.029 MPa.
c. 1.43 MPa.
d. 22.92 MPa.
e. 18 MPa.
a. Be reduced by 50%.
b. Be the same.
c. Be doubled.
d. Be increased by 141%.
e. Be increased by 400%.
See the Answers
1: d.
Use Eq. 2.4 to determine torque: T = P • K / N = 25 kW • 9,549 / 1,550 = 154 Nm. Use Eq. 3.11 to solve for displacement. disp = 2π • T / p = 6.2832 • 154 Nm / 14 MPa = 69.1 cc. Determine flow using Eq. 2.7. Q = disp • N / K = 69.1 • 1,550 / 1,000 = 107 lpm.
2: d.
Use Eq. 2.13: F1 • L1 = F2 • L2 to determine the force. F2 = F1 • L1 / L2 = 45 kN • 2 m / 0.5 m = 180 kN. To convert kN to N, multiply by 1,000. 180 • 1,000 = 180,000 N. Next, solve for the area of the piston using Eq. 2.13: A = 0.7854 • d2 = 0.7854 • 1002 = 7,854 mm2. Use Eq. 2.1 to solve for pressure: p = F / A = 180,000 N / 7,854 mm2 = 22.92 MPa.
3: d.
The flow through an orifice changes in proportion to the pressure drop across the orifice and is described as
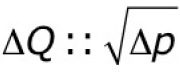In this case the Δp has doubled and so the Q will increase by the square root of 2 which is 1.414. The answer is in percentage. 1.414 • 100% = 141.4%. The best answer is 141%.
Visit www.ifps.org for more information.
Share this information.
Related Posts
June is Safety Awareness Month!
Understanding Hydraulic Stiffness of a System
Sustainable Solution: A Versatile Hydraulic Option
High-Pressure Washdown Pneumatic Valves Improve Machine Performance
Unlocking Versatility: Pneumatic Grippers Revolutionize Electric Robots With Cost-Effective Precision
2017 ICUEE
One thought on “IFPS Upgrades Hydraulic Specialist Certification”
Leave a Reply
Sponsor
Sponsors
Regards,
I have a doubt about the question 3 ,I think there is a mistake in the formulation:
“When the inlet pressure to a proportional valve is doubled with no change to the outlet pressure, the resultant flow will”
If initially we have Δp = (P1 – P2), and now we have Δp = [(2*P1) – P2] , that doesn’t mean that Δp has doubled. Then, it would not be true that the flow increases by 141%.
I think to say “with no change to the outlet pressure” is the problem . But, my apologies in advance if I made a mistake in the interpretation of the question.
Thank you, I love fluidpower journal!