Power Factor
For the purpose of this article, I would like you to divide yourselves into two groups: the “Energy Suppliers” and the “Energy Consumers.” While you are deciding which group you want to be in, I will give some introductory comments. Oh, and you should still have your calculators handy from the last article.
A country preacher was once asked how it was that he had been so successful in teaching his congregation. He responded by saying, “First, I tell them what I’m going to tell them. Then, I tell them. Then, I tell them what I told them.”
I plan to accomplish two things as a result of this article. First, I plan to raise the level of understanding of “Power Factor” for those of us who do not have a good handle on it. I will do this by giving an illustration rooted in fluid power concepts. This will lead to the second result. The illustration will highlight an area of fluid power design where we often do a poor job. The overall result will be an increased awareness in both of these subjects that will help us provide more energy efficient fluid power systems.
There, I told you what I’m going to tell you.
Are we ready? All those who chose “Energy Suppliers” raise your hands. Okay, now all who are “Energy Consumers” raise your hands. I see we are a little heavy on the “Consumer” side, but that will be all right for our discussion. It will be the job of you “Suppliers” to provide whatever the “Consumers” want. You “Consumers” can ask for anything you want, but you will have to pay for all the energy consumed.
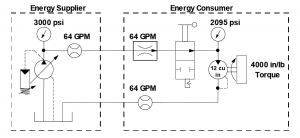
So what is this power factor thing? Well, the best way to describe it for us fluid power people is to think of a circuit provided by the “Energy Supplier” using a pressure compensated variable displacement pump. The “Energy Consumer” is driving a fixed displacement motor at a constant speed. The speed of the motor is controlled by a pressure compensated flow control set at the correct flow to match the displacement and speed required by the motor. (See the circuit below.)
To illustrate the point, we have assigned some values to the circuit. The load on the motor will be 4,000 in/lb and the speed will be 1,200 rpm. The pump compensator is set at 3000 psi. A quick calculation tells us that we will need a motor with a displacement of 8.4 cu in to meet the torque requirements. The flow from the pump will be 44 gpm and will require about 57 kW.
But we decide to be very conservative and place a motor with a displacement of 12 cubic inches in the circuit. Let’s take a look at what happens.
The larger motor will require about 64 gpm to run at 1,200 rpm, so we will set our flow control accordingly. The motor will have a ΔΔ P of 2,095 psi, which translates into 57 kW.
So what’s the problem?
For you “Energy Consumers,” it appears that you are using exactly the same energy as with the smaller motor. But we need to examine this from the point of view of an “Energy Supplier.” Take a look at what you “Suppliers” have to provide. Remember, you are using a pressure compensated pump set at 3,000 psi. You “Energy Suppliers” will have to produce the 64 GPM, but you will produce it at the compensated pressure of 3,000 psi resulting in a power requirement of 84 kW.
This is exactly the kind of thing that happens when we fluid power professionals apply an oversized electric motor for our equipment. As mentioned in earlier articles, when we apply an electric motor that is oversized, we wind up using more energy than is necessary. We tend to ignore this because we are not usually the ones responsible for paying the energy bill. The wasted energy does not show up in meters that we use because we focus on the kW at the motor and not on what the power company has to do to provide those kW.
The difference between the energy required from the power company and the energy actually used by the motor is called the “Power Factor.” This is described as the relationship between the power used by the motor and the power supplied by the power company and is given as a percentage. The ideal would be a power factor of 100% but is typically accepted as reasonable when the power factor is about 80%. This means that the power company would have to generate 20% more power than was actually being used. In our Fluid Power illustration, you “Suppliers” had to generate about 31% more energy than was actually used by the “Consumers.”
There is not an exact correlation between the flow and pressure of our fluid power system and what the power companies experience. Electric motors are driven by an alternating system that at one moment induces a magnetic field and the next moment has the magnetic field collapse. There are iron losses and copper losses and a host of other issues that are beyond the scope of this discussion. They describe their power production in terms of VAR (Volt-Amp-Reactive) while we tend to only think of the kW on our end. The point is this: just like you “Suppliers” had a production requirement that was greater than what the “Consumers” actually needed, power companies have a greater burden than is seen simply from the kW meter.
Now the folks at the power companies are generally really nice people, but they have to answer to stockholders or government agencies and so need to show a positive bottom line. They cannot afford to supply the extra power for nothing. What they do is keep a record of the kW used by the equipment and then tack on a power factor charge that covers the additional energy consumed in the process. We do not usually see this, and so we do not usually consider it when we specify or apply an electric motor. The companies that use the motors that we have specified see the add-on but often do not associate the charge directly to our equipment. It gets buried in the cost of running the facility, and we are not held responsible.
As fluid power professionals, we need to become aware of the impact our choices make on the energy cost of fluid power.
Now, I’ve told you.
There are two things that we can take from this discussion. First, using an oversized electric motor in our circuits has a direct impact on the utility bill for the fluid power user. Second, using a pressure compensated pump without due consideration for the pressure requirements of the actuators is also an energy waster. As fluid power professionals, we need to be aware of these opportunities to improve our image and the efficiencies of the fluid power systems we apply.
There, now I’ve told you what I told you.
Share this information.
Related Posts
Sponsor
Sponsors