What is the Real Size of that Pump?

Revisions to ISO 8624: A standard for determination of the derived capacity of hydraulic pumps and motors

By Jose M. Garcia-Bravo, CFPS, and Jason Nicholson

Hydraulic pumps and motors are used in a wide number of systems from mobile to industrial markets. The integrators of such systems must consider the performance characteristics of the pump or motor used when designing these systems to efficiently and safely complete a task. A study [1] of the impact of fluid power usage in the USA estimated the average efficiency of a hydraulic system is 22% and as low as 14% in certain mobile applications. Today’s market is so competitive that it demands higher efficiency compared to the last 60 years. Part of improving the efficiency of a system is selecting and operating its components to function at their peak performance. However, the selection process (in practical engineering terms) should be driven by the performance characteristics of the component as they are presented in a data sheet, such as in graphical form or in a table. When selecting a pump or a motor to perform a job, the engineer must account for the efficiency of the component.

Determining Efficiency

Determining the efficiency of a pump or a motor based on test data requires knowledge of the derived capacity (aka: derived displacement) of the machine. There are several methods for estimating or “deriving” the displacement of a pump or motor, but some of those are more accurate than others.

Currently, the ISO standard (ISO 8426-2008) for the determination of the pump or motor derived capacity uses the zero-pressure intercept method. The zero-pressure intercept method is speed-dependent, even though one of the assumptions of this method is the derived capacity’s speed independence.

Zero-pressure Intercept Method

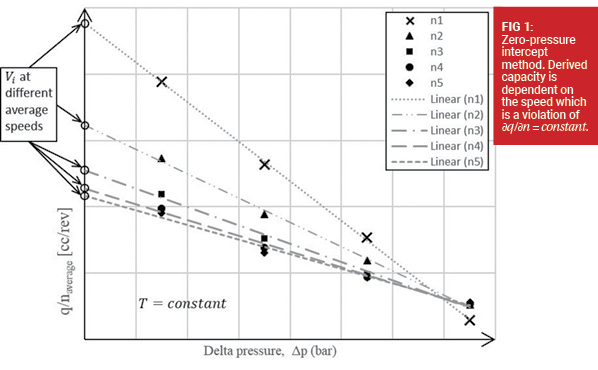
The zero-pressure intercept method uses the term high pressure flow q divided by speed n, to represent displacement Vi which is only valid if the change of flow with respect to change of speed is constant. That is, ∂q/∂n = constant = V_i   which implies that q = V_i · n  and thus V_i = q/n.

However, the zero-pressure intercept method violates this assumption if you apply it at different speeds, as shown in Figure 1. This is best seen when comparing the derived capacity at low speed vs high speed for the same machine. Put another way, this method assumes the intercept does not change when going from low speed to high speed. Often differences of 8-10% in the derived capacity calculation are common between the derived capacity at low speed vs high speed using the zero-pressure intercept method. The consequence of this assumption is that the estimated derived capacity is problematic, sometimes resulting in estimated volumetric or torque efficiencies of over 100% (a clear violation of the first law of thermodynamics!).

Revising the Standard

For that reason, a group of fluid power experts has been charged to revising this standard. The work began in September of 2017 and has concluded that a better available method is the calculation of the derived displacement using the Toet [2] method. The Toet method is a two-step method that more accurately estimates the displacement of a pump or motor [3]. The zero-pressure intercept method is depicted in Figure 1.

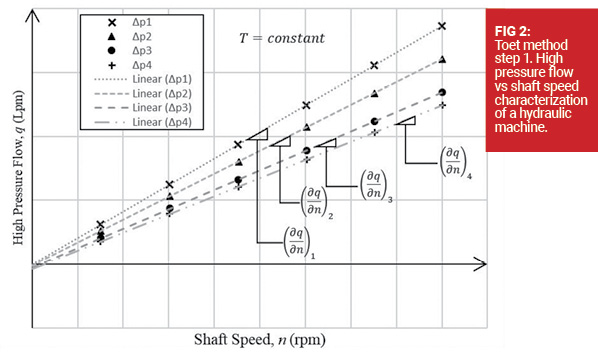
The first step of the Toet method requires the calculation of the slope, (∂q/∂n)_i  , of the high pressure flow vs. shaft speed from a linear fit for a fixed Δp_i  . This process is repeated for several Δp_i  as shown in Figure 2. The second step of the method calculates the intercept of  ∂q/∂n  vs. Δp line which corresponds to the derived capacity, V_i . The second step is shown in Figure 3.

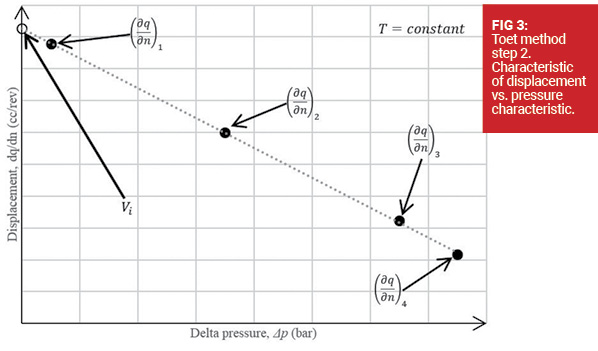
The advantage of this method is the consistency of the results at various temperature levels, T , implying independence of temperature. Unlike the zero-pressure intercept method, the speed dependence of derived capacity does not exist in the Toet method. The proposed revisions to the standard will be discussed with various international experts in fluid power and will possibly be taking effect before 2020.

References:

[1] Love, Lonnie J. Estimating the Impact (Energy, Emissions and Economics) of the US Fluid Power Industry. No. ORNL/TM-2011/14. Oak Ridge National Laboratory (ORNL), 2012.

[2] Toet, G., 1970. Die Bestimmung des theoretischen Hubvolumens von hydrostatischen Verdrängerpumpen und Motoren aus volumetrischen Messungen. Ölhydraulik und Pneumatik 14. Nr. 5, 185–190.

[3] Post, W.J.A.E.M., 1996. Models for steady-state performance of hydraulic pumps: determination of displacement. 9th Bath International Fluid Power Workshop, University of Bath, UK, Vol. 9, p. 339.

• hydraulic motors
• hydraulic pumps
• iso
• standards