Understanding Hydraulic Stiffness of a System

Hydraulic Stiffness

It is generally misunderstood that hydraulic fluid is incompressible when, in fact, it can compress when placed under pressure.

Any system components containing compressible fluid will display the behavior of a spring, and can be treated as a spring, when determining the dynamics of the system. A spring is in effect, a capacitance component, since it can store and deliver power in the same manner as a capacitor in an electrical system.

The stiffness of a spring is determined by the spring constant. The larger the constant, the stiffer the spring.

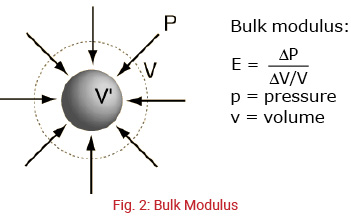
The stiffness of a hydraulic fluid is the ratio of its decrease in volume, as a result of a pressure increase and is given by its bulk modulus of elasticity.

The bulk modulus for hydrocarbon-based hydraulic fluids (E) is approximately 200,000 to 250,000 PSI, which results in a volume change of around 0.4 to 0.5% per 1,000 PSI.

E = ΔP x V / ΔV

E = 2.5 x 105 lb/(in2) = Bulk modulus of elasticity for typical hydraulic fluid

In any system with high loads, high speeds, and dynamic behavior, the stiffness of the fluid must be considered. The stiffness of the system will impact the response of the actuators to command input from the controlling components. Failure to understand the basic effects of this stiffness can lead to inappropriate selection of control components. In this section, this manual will develop the equation for approximating the stiffness of a linear actuator containing compressible hydraulic fluid.

The actuator in Fig. 3 will behave much like a spring because of the capacitance of the hydraulic fluid. The stiffness of the actuator will be a combination of several factors:

1. The bulk modulus of elasticity of the fluid (E, lb/in2).

2. The area of the piston (A1, in2).

3. The volume of the fluid (V, in3).

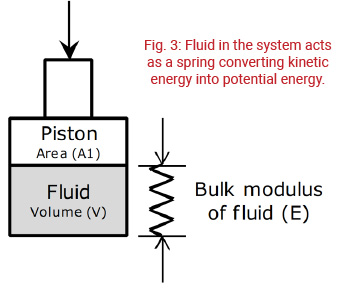Since the modulus of elasticity is fixed (as long as there is no entrained air in the fluid), the shape of the cylinder in Fig. 3 will determine the stiffness of the component with the stiffness increasing with increasing area, and decreasing with increasing volume. In fact, the stiffness will change as the cylinder extends and retracts.

The stiffness of any hydraulic component can be calculated with the following equation:

Stiffness of a hydraulic actuator

CH = E(A1)2  
              V

Take particular note of the effect that increasing the area has on increasing the stiffness of the system. The relationship has stiffness increasing as a function of the square of the area. Increasing the area has a greater effect in increasing the responsiveness of a cylinder system than decreasing the length. Note also that stiffness is inversely proportional to the volume of oil in the system.

Example

Given:

• E = 2.5 x 105 lbf/in2
• Cylinder Bore (piston): 3.00
• L = 3 in

Determine:

Stiffness of the piston on downward compression of the rod from current position

Solution:

A1 = D2 x .7854 = 3.002 x .7854 = 7.07 in2

V = A x L = 7.07 in2 3 = 21.21 in3

CH = 2.5 x 105 7.072  = 5.89 x 105 lbf /in
               21.21in3

Test Your Skills

Given:

• E = 2.5 x 105 lb./in.
• Piston diameter = 1.50 inches
• L = 5 inches

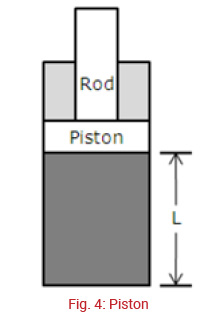
Determine: Stiffness of the piston shown in Fig. 4 on downward compression of the rod from current position.

a. 0.9 x 104 lbf / in.

b. 1.8 x 104 lbf / in.

c. 8.84 x 104 lbf / in.

d. 1.8 x 105 lbf / in.

e. 9.1 x 105 lbf / in.

Find out the solution

• basics
• hydraulic
• hydraulic fluid
• ifps